Vater,
der Du das verborgene Licht aller Lichter,
der unwandelbare Eine hinter aller Vielfalt,
das unteilbare Substrat aller Formen, Zahlen und Klänge,
die höchste Wirklichkeit aller Namen
und das Wesen aller Geschöpfe bist –
Die sei Lob, Anbetung und Ehre.
Du, der Du das Leben alles Lebendigen,
der Quell aller Farben und Töne,
der schweigende Urgrund aller Melodien, Rhythmen und Klänge,
der Ursprung aller Sprachen und Lieder,
das eine Sein aller Namen und Formen,
der eine Schöpfer aller Geschöpfe,
die eine Wahrheit hinter allen Religionen,
das Licht unseres Leibes
und das geheime Glück unseres Herzens bist –
vor Dir verneige ich mich.
Entferne den Schleier von Unwissenheit und Verblendung,
der unsere Herzen bedeckt und
offenbare uns Dein wahres, leuchtendes Wesen,
verborgen hinter dem Glanz der Natur,
Dein erhobenes Antlitz im Wandel der Schöpfung,
Deinen weisen Plan im Gang unseres Lebens
und das Licht des Ich Bin im Brautgemach unserer Seele.

Die moderne Zahlenmystik – die geometrische Vereinigung von
Kunst und Wissenschaft

Die folgende Ausführungen basieren auf dem Buch Philomath von Robert Edward Grant.
Aus kopierschutzrechtlichen Gründen habe ich die Abbildungen, die in dem Buch zu finden sind zum Teil per Hand nachgezeichnet.

Der Schlüssel zum tieferen Verständnis der Schöpfung
– I –

Seit Anbeginn der Zeit haben die Menschen gezählt. Sie zählten ihre Finger und Dinge ihres Haushalts sowie ihr Vieh. Sie zählten die Tage, Wochen und Monate, um zu wissen, wann die Zeit der nächsten Aussaat gekommen war.
Ob bewusst oder unbewusst, die Idee von Zahlen war schon immer im menschlichen Geist verankert. Im Alten Testament findet man die Zeile: „Die Macht Israels kommt von den Zahlen, denn Gott hat alles mit Gewicht, Maß und Zahl gemacht.“ (Buch Numeri). Und Pythagoras Sagte: „Die Zahl ist der Vater der Götter und der Menschen.“ Überall in der Schöpfung lassen sich Zahlenverhältnisse erkennen, die wunderbar anmuten. Bereits in früheren Zeiten haben die Menschen den Zahlen daher magische Kräfte zugeordnet.
Ursprünglich wurden Zahlen in begrenzten Begriffen wie eins, zwei und viele ausgedrückt. Seitdem haben sie sich jedoch stark vermehrt und sich bis ins Unendliche ausgedehnt.
Die Beziehungen, die der Mensch zwischen der Welt und den Zahlen entdeckte, waren zahlreich und grundlegend. Von den eigenen Körpermaßen über Pflanzen, Samen und Erträge bis hin zu den Zyklen des Mondes sowie den Bahnen von Sonne und Planeten. All dies weckte in ihm das Gefühl einer tieferen Verbindung und eines verborgenen Sinns hinter dem Universum. Zudem erkannte er, dass Geometrie und Zahlen keine getrennten Erscheinungen sind. Vielmehr sind sie untrennbar miteinander verbunden Teile des Ganzen. Kann man sich eine fünfeckige Blüte vorstellen, ohne unwillkürlich an die Zahl fünf zu denken? Die Fibonacci-Folge ist in ihrem Wesen rein numerisch, doch sobald ihre Zahlen in räumliche Dimensionen übertragen werden, entsteht eine wunderschöne Spirale, die in der Natur allgegenwärtig ist. Fundamentale Konstanten wie π oder der Goldene Schnitt Φ sind unendliche Zahlen, die geometrische Formen bestimmen. Tatsächlich beruhen fast alle Formen, die uns Menschen als harmonisch oder bedeutungsvoll erscheinen, auf solchen „magischen“ Zahlen oder fundamentalen Konstanten.

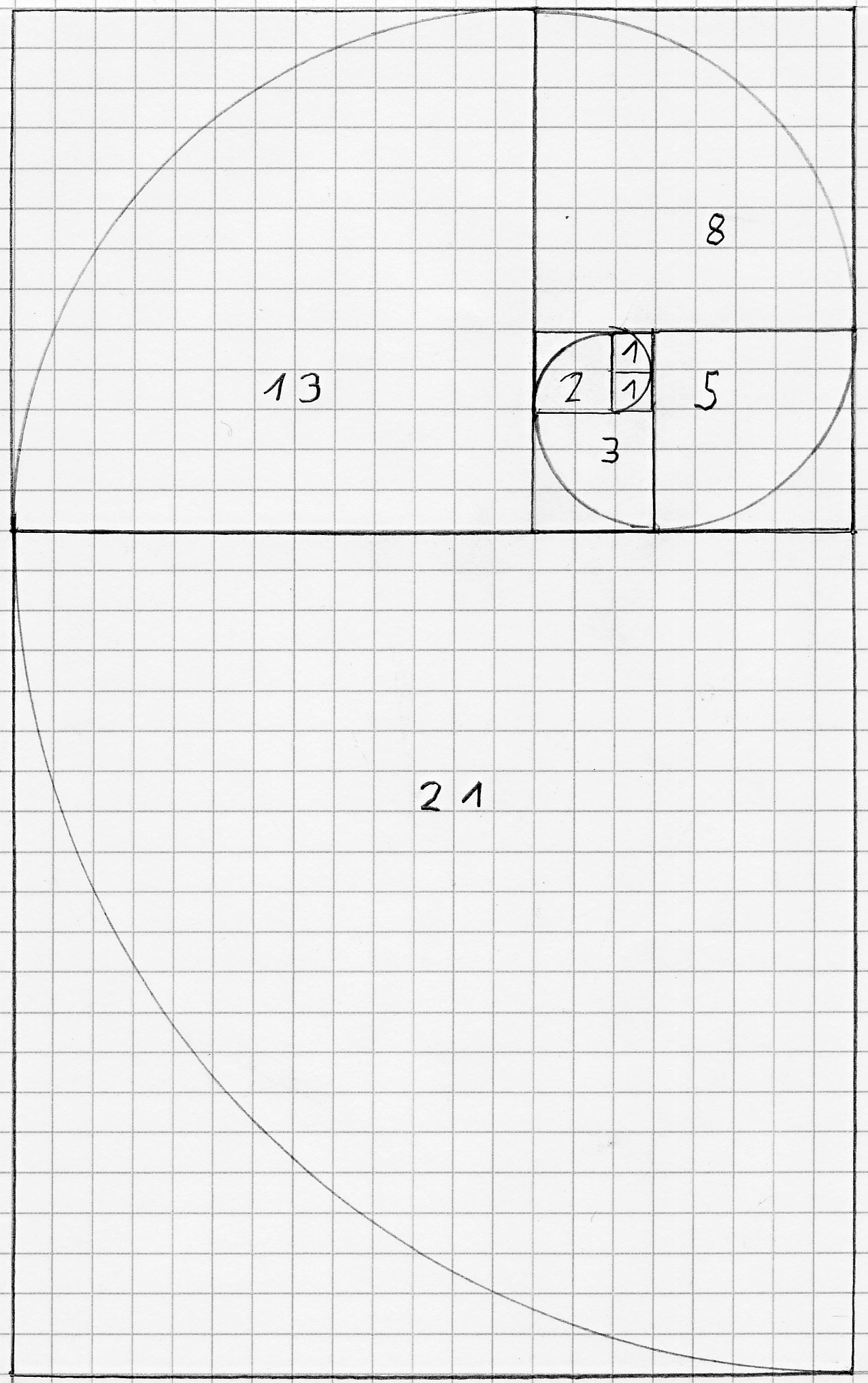
Die hier dargestellt Spirale beruht auf der Fibonacci-Folge:
1, 1 , 2, 3, 5, 8, 13, 21, …

Wenn Zahlen und Geometrie aus derselben Quelle entspringen, muss es einen Grund geben, warum bestimmte Zahlen-Form-Kombinationen für bestimmte Manifestationen in der Natur gewählt wurden. So begann der Mensch, in der Natur ein Rätsel zu erkennen – eine göttliche Verschlüsselung, deren Schlüssel überall verstreut liegen, verborgen in den komplexen Schichten der Welt, die er mit seinen Sinnen wahrnimmt.
Wenn wir geometrische Muster mit unseren Augen erfassen, werden sie in unserem Gehirn häufig in Zahlen übersetzt. Etwa die 3 für ein Dreieck, die 4 für ein Quadrat und so weiter. Formen, die sich nicht auf diese Weise beschreiben lassen, empfinden wir meist als zufällig oder unregelmäßig. Möglicherweise arbeitet unser Gehirn genau auf diese Weise. Es übersetzt alles unbewusst in Zahlen und Verhältnisse und entscheidet auf dieser Grundlage über Proportion, Abstand, Gleichmäßigkeit und Harmonie. Und wenn diese Verhältnisse auf besonderen, „magischen“ Zahlen beruhen, dann reicht die Erfahrung über den Verstand hinaus und berührt unsere Seele.
Zahlen sind somit ein Kanal, über den Sehen, Denken und Empfinden miteinander verbunden sind. In diesem Sinne entdeckte der Mensch die zweite Ebene der göttlichen Verschlüsselung –  die Geometrie, während die erste Ebene aus den Zahlen selbst besteht.
Das Hören ist der nächstwichtige Sinn des Menschen (manche würden sogar behaupten, es sei der wichtigste). Auch das Phänomen des Klangs lässt sich durch Zahlen beschreiben. Frequenz, Tonhöhe, Amplitude und vieles mehr. Doch damit eine Kombination von Tönen als angenehm und harmonisch empfunden wird – damit aus Klang Musik entsteht –, müssen die Zahlen, die sie beschreiben, in bestimmten Verhältnissen zueinander stehen. Genau dies soll Pythagoras vor über zweitausend Jahren erkannt haben. Bestimmte Zahlenverhältnisse erzeugen Wohlklang, andere nicht. Auch wenn das Hörerlebnis an sich nicht ausschließlich auf Zahlen beruht, hängt das, was wir als schön und berührend empfinden, stark von ihnen ab. In diesem Sinne sind Geometrie und Klang einander ähnlich. Damit sie vom Gehirn als stimmig wahrgenommen werden und mit der Seele in Resonanz treten, müssen sie bestimmten Zahlen und Proportionen entsprechen. So entdeckte der Mensch die dritte Ebene der göttlichen Verschlüsselung – Klang und Musik.
Jene Zahlen, die der Mensch immer wieder in der Natur beobachtete – sei es in Form oder Klang –, nahmen einen besonderen Platz in seinem bewussten und unbewussten Denken ein. Man betrachtete sie als magisch, als Ausfluss eines göttlichen Intellekts, der sich in wunderbaren Schöpfungen in unserer Welt manifestiert. Aus dieser Überzeugung heraus begannen Wissenschaftler, Philosophen und Künstler, diese Zahlen bewusst in ihre Werke einzubauen – sei es in Bücher, Gemälde oder musikalische Kompositionen. Viele Autoren strukturierten ihre Werke nach bestimmten Zahlenfolgen, etwa der Fibonacci-Reihe, oder versteckten Hinweise durch Wortwiederholungen oder hervorgehobene Buchstaben. Manche Musiker sollen ihre Kompositionen nach spezifischen Zahlenverhältnissen und mathematischen Konstanten wie dem Goldenen Schnitt aufgebaut haben.
Doch niemand nutzte die Kraft der Zahlen so intensiv wie Maler und Architekten. In der visuellen Kunst fanden Zahlen einen besonders fruchtbaren Boden, um tief verankert zu werden – sei es in einem Gemälde oder einem Bauwerk. Sie verliehen ihm Energie, Harmonie für den Betrachter und verbargen zugleich Botschaften und Hinweise, die mitunter erst nach Jahrhunderten oder Jahrtausenden von wachsamen Suchenden entdeckt wurden.
Antike Bauwerke und Tempel sind lebendige Zeugnisse der zahlenverliebten Geister hinter ihrer Entstehung. Monumente wie die Große Pyramide von Gizeh oder der Parthenon in Griechenland sind durchzogen von Naturkonstanten wie π, e oder Φ. Um diese Zahlen in die Gestaltung und Dimensionen ihrer Bauwerke einzubetten, benötigten Architekten und Baumeister tiefes mathematisches Wissen und hohe ingenieurtechnische Fähigkeiten. Magische Zahlen waren daher nicht nur das Ergebnis aufmerksamer Beobachtung und Kontemplation, sondern trieben auch die Entwicklung fortgeschrittener Mathematik, Technik und Wissenschaft voran.
Die letzte Ebene der göttlichen Verschlüsselung offenbarte sich in den Naturwissenschaften. Hier stellte man fest, dass zahlreiche fundamentale Zahlen – sogenannte Konstanten – das Leben und das gesamte Universum steuern, wie etwa die Feinstrukturkonstante α, die die Wechselwirkung von Licht und Materie bestimmt; die Eulersche Zahl e, die radioaktiven Zerfall und viele andere Prozesse beschreibt, die Planck-Konstante h oder die Coulomb-Konstante C. Die Quantisierung der atomaren Welt öffnete die Tür zu einem faszinierenden und geheimnisvollen Reich, in dem Zahlen uneingeschränkt herrschen. Alles im Atom wird durch spezifische Quantenzahlen bestimmt, die das Verhalten seiner Elektronen, Protonen und Neutronen beschreibt. Einige dieser Zahlen sind so besonders, dass sie selbst von Wissenschaftlern als „magisch“ bezeichnet wurden – etwa die magischen Zahlen der Atomkerne: 2, 10, 18, 36, 54 und 86. Bemerkenswert ist, dass viele dieser Zahlen bereits seit Jahrtausenden bekannt und geschätzt wurden, lange bevor ihre mikroskopische Bedeutung erkannt wurde.
Mit Geometrie, Klang und Wissenschaft – vereint durch Zahlen – war die göttliche Verschlüsselung vollständig. Es war der richtige Moment, die Schlüssel zu finden und den Code zu entschlüsseln. Doch dieses Wissen entstand in einer Zeit, in der Zahlen zunehmend ihrer Bedeutung und Symbolik beraubt wurden. Sie wurden zu bloßen Werkzeugen der Berechnung degradiert und ihrer eigentlichen Kraft beraubt, alle Sinne zu vereinen und Wissen in einer ganzheitlichen Matrix zusammenzuführen.
Entsprechend dieser nüchternen Haltung wurden Lehrpläne an Schulen und Universitäten so gestaltet, dass der wahre Zweck der Zahlen weitgehend ausgeklammert blieb. Wissenschaftliche Disziplinen wurden immer weiter fragmentiert und spezialisiert, wodurch der Suchende den Zugang zum eigentlichen Ziel der Wissenschaft und zu ihrem ganzheitlichen Nutzen verlor. Fragmentierung wurde zum Geist der Zeit.Aus unserer Liebe zu den Zahlen und der Bedeutung, die sie unserem Verständnis des Universums verleihen, begaben wir uns auf eine Reise des Lernens durch Raum und Zeit, auf der wir erstaunliche Entdeckungen machen werden. Ihr Ziel ist es, dieses Wissen der Allgemeinheit wieder zugänglich zu machen. Dabei sind wir davon überzeugt, dass die Menschheit heute mehr denn je ihre fragmentierte Denkweise überwinden und eine natürliche, ganzheitliche Sicht auf das Universum wiederentdecken muss.

Über die Eigenschaften von Zahlen

Wir beginnen die Suche nach den tieferen Mustern und Strukturen der Schöpfung, indem wir Zahlen größer als 0 auf eine einzige Ziffer reduzieren. Diese erhalten wir dadurch dass, wir die Quersumme der jeweiligen Zahl bilden. Dieses Verfahren wiederholen wir so oft, bis nur noch eine Ziffer übrig bleibt.
Die Quersumme einer Zahl Q(X) erhalten wir indem wir die Summe der einzelnen Ziffern der Zahl X bilden.
Beispiel: Wir bilden die Quersumme der Zahl 6821 → Q(6821) = 6 + 8 + 2 + 1 = 17
Da die Zahl 17 als erste Quersumme von 6821 aus 2 Ziffern besteht, wenden wir das Verfahren noch einmal an,
wir bilden also die Quersumme von 12 → Q(12) = 1 + 2 = 3
Die Quersumme von 6821 ist letztendlich 3.
Dieses Verfahren funktioniert auch mit endlichen Dezimalbrüchen.
Durch das Quersummen-Verfahren erhalten wir nur Werte von 1 bis 9. Die Null kommt nicht vor, da wir nur Zahlen betrachten, die größer sind als Null. Die so entstandenen Ziffern bezeichnen wir als Grundziffern. Es entsteht folgendes Bild, bei dem Zahlen, die übereinander stehen, die gleiche Quersumme besitzen:

Das Rad der Grundziffern

Die Grundrechenarten im Rad der Grundziffern

Addition und Subtraktion:
Wenn a  + b + c + … = d, dann ist Q[ Q(a) + Q(b) + Q(c) + … ] = Q(d).
Beispiel:
687 + 5210 + 847 = 6744
→ Q(687) + Q(5210) + Q(847) = 21 + 8 + 19 = 48 → Q(48) = 12 →  Q(12) = 3
und Q(6744) = 21 → Q(21) = 3
Die Summe der einzelnen Quersummen ist also gleich der Quersumme der Summe der addierten Zahlen.

Analog verhält es sich bei der Subtraktion.

Multiplikation:
Wenn a x b x c = d, dann ist Q[ Q(a) x Q(b) x Q(c) x … ] = Q(d).
Beispiel: 35 x 23  x 342 = 275310
→ Q(35) = 8 und Q(23) = 5 und Q(342) = 9 → Q(8 x 5 x 9) = Q(360) = 9
und Q(275310) = 18 → Q(18) = 9

Division:
Bei der Division verhält es sich nicht ganz so einfach, weshalb ich hier nicht weiter darauf eingehe.

Die besondere Bedeutung der 9

Da die 0 unter den Grundziffern nicht vorkommt, übernimmt die 9 hier die Aufgaben der 0.
Addiert man die 9 zu einer beliebegen Zahl, verändert sich nicht ihre Grundziffer. Beispiel: Q(34) = 7, Q(34 + 9) = Q(43) → Q(43) = 7

Bei der Multiplikation einer Zahl mit 9, erhält man für die Grundziffer immer 9. Genauso wie man bei der „echten“ Multiplikation mit 0 immer 0 erhält.
Beispiel: 56 x 9 = 504 → Q(504) = 9 und 57 x 9 = 513 → Q(513) = 9

Die 9 stand symbolisch immer schon für Vollständigkeit. Sie steht für den Anfang und das Ende von Zeitaltern. So wandert der Tierkreis alle 72 Jahre um ein Grad durch den Nachthimmel. Q(72) = 9 ein voller Umlauf dauert (360 x 72) =  25920 Jahre dabei ist Q(25920) = 9

Der Kreis der Grundziffern

Wenn wir die Grundziffer wie in folgendem Kreis anordnen, können wir einige interessante Eigenschaften erkennen. So teilen die Ziffern 3, 6 und 9 den Kreis in drei Segmente, wobei die Summe der Ziffern in jedem Segment wieder gleich 3, 6 oder 9 ist.

Q(1 + 2) = 3
Q(4 + 5) = 9
Q(7 + 8) = 15 → Q(15) = 6

Der Kreis der Grundziffern

Außerdem ist die Quersumme von Ziffern, die sich gegnüber liegen wieder gleich 9.
Q(1 + 8) = 9
Q(2 + 7) = 9
Q(3 + 6) = 9
Q(4 + 5) = 9

Der unendliche Weg durch den Kreis der Grundziffern

Es gibt einen unendlichen Weg durch den Kreis der Grundziffern, der sich in der Verdoppelung der Grundziffern offenbart. Wir starten bei der 1,  verdoppeln diese und erhalten 2. Nun verdoppeln wir die 2 und erhalten 4. Das Verdoppeln der 4 bringt uns zur 8. Wenn wir nun 8 verdoppeln, erhalten wir 16. Die 16 kommt nicht vor, aber Q(16) ist gleich 7. Wir gehen also von der 8 zur 7. Die Verdoppelung von 7 bringt uns zur 14, die ebenfalls nicht vorkommt, aber auch hier gilt, Q(14) ist gleich 5. So kommen wir von der 7 zur 5. Das Verdopeln der 5 ergibt 10, die wieder nicht vorkommte, doch Q(10) ist gleich 1. Der Weg führt also von der 5 zurück zur 1 und der Kreis schließt sich.

Yin und Yang

Wenn man den Kreis der verdoppelten Grundziffer in der richtigen Reihenfolge – 1, 2, 4, 8, 7, 5, 1 – anordnet, erhält man das Symbol für Yin und Yang. Auf der dunklen Seite stehen die geraden Zahlen, auf der hellen Seite die ungeraden. Wenn wir nun die Summe der geraden Zahlen bilden, erhalten wir 2 + 4 + 8 = 14 und Q(14) = 5. Aus der Summe der geraden Zahlen entsteht eine ungerade Zahl. Und wenn wir die Summe der ungeraden Zahlen bilden erhalten wir 1 + 5 + 7 = 13 und Q(13) = 4. Wir erhalten eine eine gerade Zahl. Dabei gilt: 4 + 5 = 9

Auch die Zahlen, die sich diagonal gegenüber liegen – also immer eine gerade Zahl und eine ungerade Zahl ergeben die Summe 9.

1 + 8 = 9
2 + 7 = 9
4 + 5 = 9
5 + 4 = 9
7 + 2 = 9
8 + 1 = 9

Im Diagramm von Yin und Yang werden die wirkenden Kräfte der Welt, wie weiblich und männlich, positiv und negativ, gleichwertig und ausgewogen dargestellt. Man findet diese beiden Prinzipien in allem, was existiert. Weil Yin und Yang nicht statisch sind, sondern sich ständig gegenseitig beeinflussen, sieht man in dem Diagramm den Keim des einen in seinem Gegenpol enthalten. In dem Diagramm erkennt man dies an dem schwarzen Punkt im weißen Feld und dem weißen Punkt im schwarzen Feld. Das Symbol von Yin und Yang steht für Vollständigkeit. Wobei in den Gegensätzen der Kern des Anderen steckt, was zusammen die Einheit zeigt. Die Zahlen offenbaren uns hier eine alte Weisheit.

Die Magie der Primzahlen

Wir können die Zahlen nicht nur in gerade und ungerade unterteilen, sondern wir können sie in Primzahlen und zusammengesetzte Zahlen unterteilen. Primzahlen sind natürliche Zahlen, die genau 2 Teiler haben. Sie sind durch 1 und sich selbst teilbar. Die 1 ist keine Primzahl, da sie nur einen Teiler hat. Somit ist die 2 die kleinste Primzahl und sie ist die einzig gerade Primzahl. Alle geraden Zahlen mit Ausnahme der 2 sind keine Primzahlen, sondern Vielfache von 2. Um aber die Muster und Strukturen innerhalb der natürlichen Zahlen zu verdeutlichen, soll die 1 als „Startzahl“ mit betrachtet werden. Wenn ich also im folgenden von Primzahlen spreche, mag es vorkommen, dass auch die 1 mit aufgeführt wird. Das ist mathematisch nicht einwandfrei, aber für die Mustererkennung aussagestärker. Es geht hier auch nicht um klare mathematische Beweise, sondern um das Aufzeigen von verborgenen Mustern.
Zusammengesetzte Zahler, sind Zahlen die keine Primzahlen sind. Sie haben also mindestens 3 Teiler. Die 1 als kleinsten Teiler einer Zahl und die Zahl selbst als größten Teiler der Zahl nennen wir triviale Teiler. Hat eine Zahl neben den trivialen Teilern noch mindestens einen weiteren Teiler, sprechen wir bei der Zahl von einer zusammengesetzten Zahl.
Schauen wir uns zunächst einige Teilermengen von Zahlen an. Dabei ist T_x die Teilermenge der Zahl x.
T₁ = {1}                           
T₂ = {1, 2}                       – Primzahl
T₃ = {1, 3}                       – Primzahl
T₄ = {1, 2, 4}                   – zusammengesetzte Zahl
T₅ = {1, 5}                       – Primzahl
T₆ = {1, 2, 3, 6}               – zusammengesetzte Zahl
T₇ = {1, 7}                       – Primzahl
T₈ = {1, 2, 4, 8}               – zusammengesetzte Zahl
T₉ = {1, 3, 9}                    – zusammengesetzte Zahl
T₁₀ = {1, 2, 5, 10}             – zusammengesetzte Zahl
T₁₁ = {1, 11}                     – Primzahl
T₁₂ = {1, 2, 3, 4, 5, 6, 12} – zusammengesetzte Zahl

Was wir über Primzahlen wissen

• Es gibt unendlich viele Primzahlen.
• Und es gibt keinen Algorithmus, mit dem man Primzahlen herstellen kann.
• Es ist uns auch nicht möglich, zu sagen wann die nächste Primzahl auftauchen wird.
• Aufgrund der Nicht-Vorhersagbarkeit des Auftauchens von Primzahlen, werden Primzahlen häufig zum Schutz im IT-Bereich genutzt oder beim Verschlüsseln von Nachrichten.

Semiprimzahlen

Zahlen, die aus dem Produkte zweier Primzahlen entstanden sind, heißen Semiprimzahlen. Sie haben mindestens 3 und höchstens 4 Teiler.

Beispiele:
2 x 2 = 4 → T₄= {1, 2, 4}
2 x 3 = 6 → T₆ = {1, 2, 3, 6}
3 x 3 = 9 → T₉ = {1, 3, 9}
3 x 5 = 15 → T₁₅ = {1, 3, 5, 15}
173 x 179 = 30967 → T₃₀₉₆₇ = {1, 173, 179, 30967}
997 x 997 = 994009 → T₉₉₇ = {1, 997, 994009}

30967 und 994009 sind Semiprimzahlen, die wir ganz einfach hergestellt haben. Die Teiler der Zahlen über die Primfaktorzerlegung zu ermitteln ist dann aber nicht so einfach. ChatGPT hat 30967 als Primzahl identifiziert, was falsch ist. DeepSeek hat 30967 als Semiprimzahl identifiziert und gezeigt, dass 30967 = 173 x 179. Hier kommt die KI also z.T. an ihre Grenzen.

Muster oder Zufall?

Nun stellen wir uns die Frage, ob die Verteilung der Primzahlen einem Muster folgt oder ob sie rein zufällig auftrtreten.

Jede Primzahl > 5 endet auf 1, 3, 7, 9.
Jede Primzahl > 5 kann in der Form 6k + 1 oder 6k – 1 dargestellt werden, wobei k eine natürliche Zahl ist. Das bedeutet nicht, dass ich über diese  beiden Formeln beliebige Primzahlen herstellen kann. Es gilt nur anders herum. Wenn ich eine Primzahl habe, dann kann ich sie über eine der beiden Formeln darstellen.

Beispiele:
7 = 6 x 1 + 1
11 = 6 x 2 – 1
13 = 6 x 2 + 1
17 = 6 x 3 – 1
19 = 6 x 3 + 1
23 = 6 x 4 – 1
29 = 6 x 5 – 1

Abgesehen davon, dass die 6 eine entscheidende Bedeutung für Primzahlen zu haben scheint,  gilt auch: p² = f x 24 + 1 für alle Primzahlen p ≥ 5 wobei f eine natürliche Zahl ist.

Erklärung:
Der Faktor k in p = 6k ± 1 kann gerade oder ungerade sein. Wenn wir nun k durch 2m für gerade Zahlen ersetzen und durch 2m + 1 für ungerade Zahlen ersetzen, und dann die Gleichung quadrieren, erhalten wir folgende 4 Fälle:

p² = ((6 x 2m) + 1)² = (12m + 1)² = 144m² + 24m + 1

p² = ((6 x 2m) – 1)² = (12m – 1)² = 144m² – 24m + 1

p² = (6 x (2m + 1) +1)² = (12m + 7)² = 144m² + 168m + 49

p² = (6 x (2m + 1) -1)² = (12m + 5)² = 144m² + 120m + 25

Alle ausmultiplizierten Gleichungen erhalten den Faktor 24 x am + 1, wobei a eine natürliche Zahl ist, wie z.B. in (6m² + m) x 24 +1.
Setzen wir jetzt (6m² + m) = f, erhalten wir wieder p² = f x 24 + 1.

Eine weitere Eigenschaft von Primzahlen ist die, dass ale Primzahlen, die größer als 3 sind, Quersummen besitzen, die nur die Werte 3, 6 oder 9 haben. Aus der Gleichung p² = f x 24 + 1 geht folgendes hervor:
Wenn p die Quersumme 3, 6 oder 9 hat, ist Q(p²) immer gleich 9, denn:

Q(3²) = 9
Q(6²) = Q(36) = 9
Q(9²) = Q(81) = 9

Auf der rechten Seite der Gleichung haben wir f x 24 + 1, wenn wir uns nur den Teil f x 24 ansehen, so haben wir hier immer die Quersumme 3, 6 oder 9:

Q(1 x 24) = Q(24) = 6
Q(2 x 24) = Q(48) = Q(12) = 3
Q(3 x 24) = Q(72) = 9
Q(4 x 24) = Q(96) = Q(15) = 6
Q(5 x 24) = Q(120) = 3
Q(6 x 24) = Q(144) = 9
Q(7 x 24) = Q(168) = Q(15) =6
Q(8 x 24) = Q(192) = Q(12) = 3
Q(9 x 24) = Q(216) = 9

Addieren wir nun jeweils 1 hinzu, erhalten wir immer 7, 4 oder 1 als Quersumme. Wir erhalten also nie eine 9 auf beiden Seiten der Gleichung. Eine Primzahl hat also nie eine Quersumme von 3, 6 oder 9.
Um bei einer beliebigen Zahl festzstellen, ob sie eine Primzahl ist, prüfen wir erst ob es ich um eine ungerade Zahl handelt. Wenn ihre Quersumme dann weder 3 oder 6 oder 9 ist, ist die Zahl keine Primzahl. Bei allen anderen Quersummen besteht die Möglichkeit, eine Primzahl zu sein.

Geheime Strukturen im Vedischen Quadrat

Im Hinduismus wurden mündliche Überlieferungen um 1500 -2000 v Chr. in den heiliegen Schriften – den Veden – niedergeschrieben. Ähnlich wie in der jüdischen Kabbala gibt es auch im Hinduismus einen Teil, der sich mit Zahlen beschäftigt. So kann man im Vedischen Quadrat verborgene Muster erkennen. Beim Vedischen Quadrat handelt es sich um eine Multiplikation-Tabelle von Grundziffern, die man erhält, wenn man die Quersumme einer Zahl bildet. Das Muster zeigt sich, wenn man gleiche Grundziffern miteinander verbindet. Jede Grundziffer bildet hierin ein bestimmtes Muster. Die Grundzifferpaare, deren Summe gleich 9 ist, sind Spiegelbilder voneinander. Das gilt für 1 und 8, 2 und 7, 3 und 6, 4 und 5. Die 9 steht allein.

Grundziffern im Vedischen Quadrat

Das erinnert doch stark an den kabbalistischen Baum des Lebens, der in der Mitte des Garten Edens steht. Leider wird auf ihn und seine Bedeutung in der Bibel nicht weiter eingegangen. Dennoch möchte ich ihn an dieser Stelle kurz erwähnen, da er für die Schöpfung nicht so unwichtig zu seinen scheint, er aber im Christentum keine Bedeutung hat.

Die 22 Pfade welche, die zehn Sefiroth (Sphären) im kabbalistischen Baum des Lebens untereinander verbinden, entsprechen den Großen Arkana, den Tarot-Trümpfen. Hier entspricht der erste Pfad dem Narren, der letzte Pfad der Welt. Ausserdem findet man in der kabbalistischen Sprache auch die 72 Namen Gottes. Hier taucht wieder die 72 als heilige Zahl auf, die es auch im Islam gibt. Dort allerdings in Form von 72 Jungfrauen.