Wir können die Zahlen nicht nur in gerade und ungerade unterteilen, sondern wir können sie in Primzahlen und zusammengesetzte Zahlen unterteilen. Primzahlen sind natürliche Zahlen, die genau 2 Teiler haben. Sie sind durch 1 und sich selbst teilbar. Die 1 ist keine Primzahl, da sie nur einen Teiler hat. Somit ist die 2 die kleinste Primzahl und sie ist die einzig gerade Primzahl. Alle geraden Zahlen mit Ausnahme der 2 sind keine Primzahlen, sondern Vielfache von 2. Um aber die Muster und Strukturen innerhalb der natürlichen Zahlen zu verdeutlichen, soll die 1 als „Startzahl“ mit betrachtet werden. Wenn ich also im folgenden von Primzahlen spreche, mag es vorkommen, dass auch die 1 mit aufgeführt wird. Das ist mathematisch nicht einwandfrei, aber für die Mustererkennung aussagestärker. Es geht hier auch nicht um klare mathematische Beweise, sondern um das Aufzeigen von verborgenen Mustern.
Zusammengesetzte Zahler, sind Zahlen die keine Primzahlen sind. Sie haben also mindestens 3 Teiler. Die 1 als kleinsten Teiler einer Zahl und die Zahl selbst als größten Teiler der Zahl nennen wir triviale Teiler. Hat eine Zahl neben den trivialen Teilern noch mindestens einen weiteren Teiler, sprechen wir bei der Zahl von einer zusammengesetzten Zahl.
Schauen wir uns zunächst einige Teilermengen von Zahlen an. Dabei ist Tx die Teilermenge der Zahl x.
T1 = {1}
T2 = {1, 2} – Primzahl
T3 = {1, 3} – Primzahl
T4 = {1, 2, 4} – zusammengesetzte Zahl
T5 = {1, 5} – Primzahl
T6 = {1, 2, 3, 6} – zusammengesetzte Zahl
T7 = {1, 7} – Primzahl
T8 = {1, 2, 4, 8} – zusammengesetzte Zahl
T9 = {1, 3, 9} – zusammengesetzte Zahl
T10 = {1, 2, 5, 10} – zusammengesetzte Zahl
T11 = {1, 11} – Primzahl
T12 = {1, 2, 3, 4, 5, 6, 12} – zusammengesetzte Zahl
Was wir über Primzahlen wissen
- Es gibt unendlich viele Primzahlen.
- Und es gibt keinen Algorithmus, mit dem man Primzahlen herstellen kann.
- Es ist uns auch nicht möglich, zu sagen wann die nächste Primzahl auftauchen wird.
- Aufgrund der Nicht-Vorhersagbarkeit des Auftauchens von Primzahlen, werden Primzahlen häufig zum Schutz im IT-Bereich genutzt oder beim Verschlüsseln von Nachrichten.
Semiprimzahlen
Zahlen, die aus dem Produkte zweier Primzahlen entstanden sind, heißen Semiprimzahlen. Sie haben mindestens 3 und höchstens 4 Teiler.
Beispiele:
2 x 2 = 4 → T4= {1, 2, 4}
2 x 3 = 6 → T6 = {1, 2, 3, 6}
3 x 3 = 9 → T9 = {1, 3, 9}
3 x 5 = 15 → T15 = {1, 3, 5, 15}
173 x 179 = 30967 → T30967 = {1, 173, 179, 30967}
997 x 997 = 994009 → T997 = {1, 997, 994009}
30967 und 994009 sind Semiprimzahlen, die wir ganz einfach hergestellt haben. Die Teiler der Zahlen über die Primfaktorzerlegung zu ermitteln ist dann aber nicht so einfach. ChatGPT hat 30967 als Primzahl identifiziert, was falsch ist. DeepSeek hat 30967 als Semiprimzahl identifiziert und gezeigt, dass 30967 = 173 x 179. Hier kommt die KI also z.T. an ihre Grenzen.
Muster oder Zufall?
Nun stellen wir uns die Frage, ob die Verteilung der Primzahlen einem Muster folgt oder ob sie rein zufällig auftrtreten.
Jede Primzahl > 5 endet auf 1, 3, 7, 9.
Jede Primzahl > 5 kann in der Form 6k + 1 oder 6k – 1 dargestellt werden, wobei k eine natürliche Zahl ist. Das bedeutet nicht, dass ich über diese beiden Formeln beliebige Primzahlen herstellen kann. Es gilt nur anders herum. Wenn ich eine Primzahl habe, dann kann ich sie über eine der beiden Formeln darstellen.
Beispiele:
7 = 6 x 1 + 1
11 = 6 x 2 – 1
13 = 6 x 2 + 1
17 = 6 x 3 – 1
19 = 6 x 3 + 1
23 = 6 x 4 – 1
29 = 6 x 5 – 1
Abgesehen davon, dass die 6 eine entscheidende Bedeutung für Primzahlen zu haben scheint, gilt auch: p2 = f x 24 + 1 für alle Primzahlen p ≥ 5 wobei f eine natürliche Zahl ist.
Erklärung:
Der Faktor k in p = 6k ± 1 kann gerade oder ungerade sein. Wenn wir nun k durch 2m für gerade Zahlen ersetzen und durch 2m + 1 für ungerade Zahlen ersetzen, und dann die Gleichung quadrieren, erhalten wir folgende 4 Fälle:
p2 = ((6 x 2m) + 1)2 = (12m + 1)2 = 144m2 + 24m + 1
p2 = ((6 x 2m) – 1)2 = (12m – 1)2 = 144m2 – 24m + 1
p2 = (6 x (2m + 1) +1)2 = (12m + 7)2 = 144m2 + 168m + 49
p2 = (6 x (2m + 1) -1)2 = (12m + 5)2 = 144m2 + 120m + 25
Alle ausmultiplizierten Gleichungen erhalten den Faktor 24 x am + 1, wobei a eine natürliche Zahl ist, wie z.B. in (6m2 + m) x 24 +1.
Setzen wir jetzt (6m2 + m) = f, erhalten wir wieder p2 = f x 24 + 1.
Eine weitere Eigenschaft von Primzahlen ist die, dass ale Primzahlen, die größer als 3 sind, Quersummen besitzen, die nur die Werte 3, 6 oder 9 haben. Aus der Gleichung p2 = f x 24 + 1 geht folgendes hervor:
Wenn p die Quersumme 3, 6 oder 9 hat, ist Q(p2) immer gleich 9, denn:
Q(32) = 9
Q(62) = Q(36) = 9
Q(92) = Q(81) = 9
Auf der rechten Seite der Gleichung haben wir f x 24 + 1, wenn wir uns nur den Teil f x 24 ansehen, so haben wir hier immer die Quersumme 3, 6 oder 9:
Q(1 x 24) = Q(24) = 6
Q(2 x 24) = Q(48) = Q(12) = 3
Q(3 x 24) = Q(72) = 9
Q(4 x 24) = Q(96) = Q(15) = 6
Q(5 x 24) = Q(120) = 3
Q(6 x 24) = Q(144) = 9
Q(7 x 24) = Q(168) = Q(15) =6
Q(8 x 24) = Q(192) = Q(12) = 3
Q(9 x 24) = Q(216) = 9
Addieren wir nun jeweils 1 hinzu, erhalten wir immer 7, 4 oder 1 als Quersumme. Wir erhalten also nie eine 9 auf beiden Seiten der Gleichung. Eine Primzahl hat also nie eine Quersumme von 3, 6 oder 9.
Um bei einer beliebigen Zahl festzstellen, ob sie eine Primzahl ist, prüfen wir erst ob es ich um eine ungerade Zahl handelt. Wenn ihre Quersumme dann weder 3 oder 6 oder 9 ist, ist die Zahl keine Primzahl. Bei allen anderen Quersummen besteht die Möglichkeit, eine Primzahl zu sein.
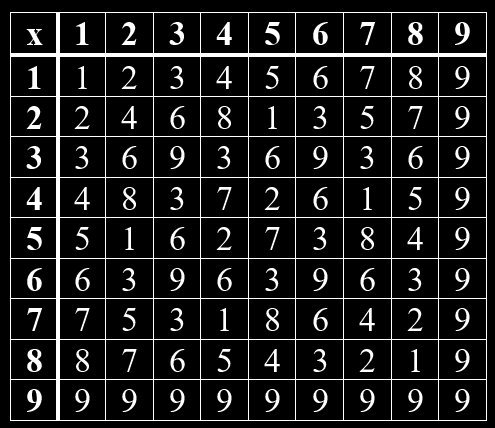
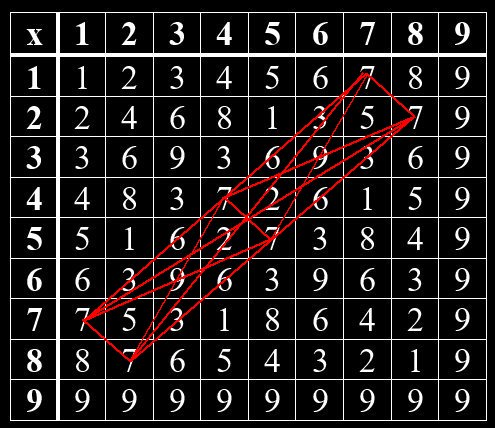
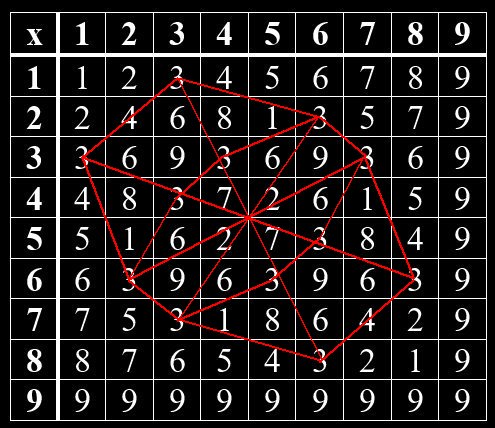
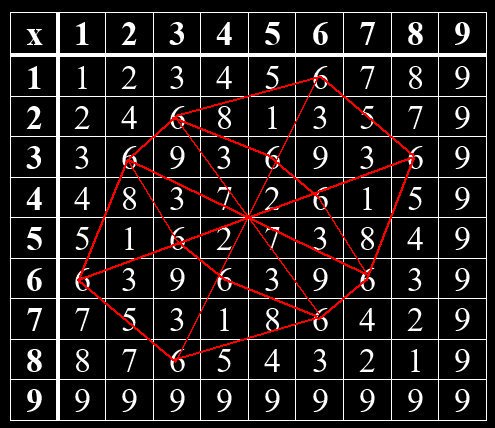
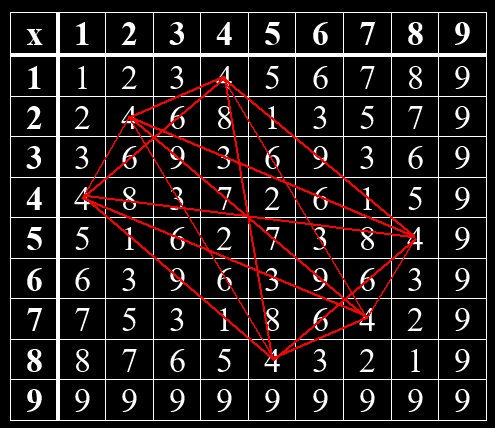
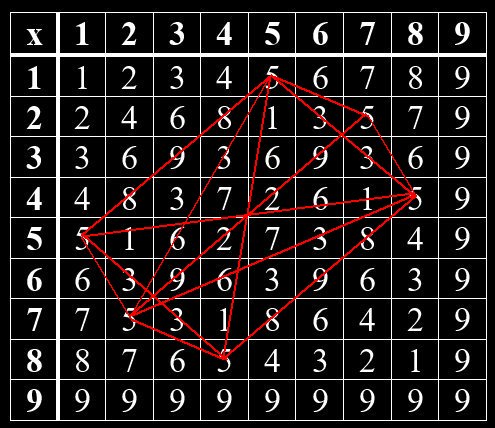
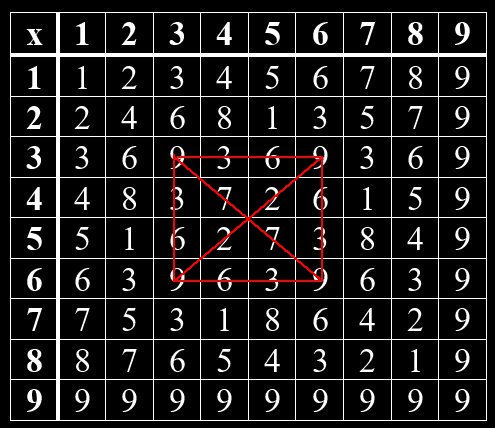
Geheime Strukturen im Vedischen Quadrat
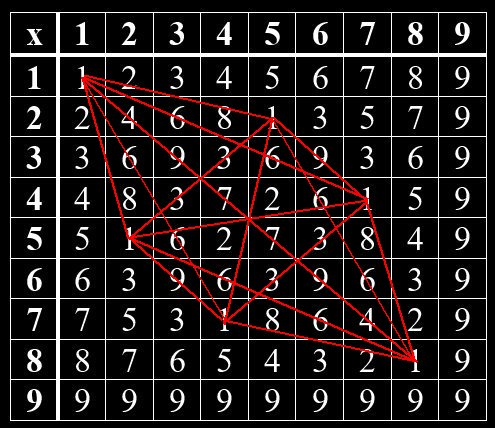
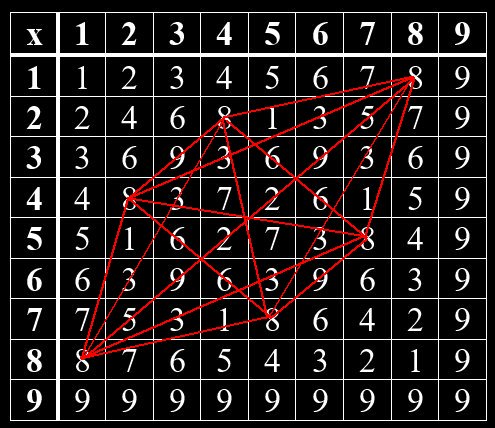
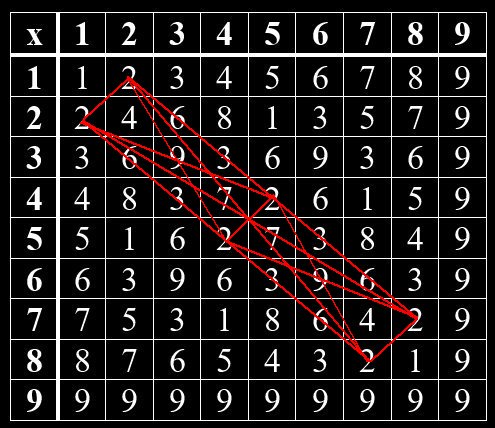
Im Hinduismus wurden mündliche Überlieferungen um 1500 -2000 v Chr. in den heiliegen Schriften – den Veden – niedergeschrieben. Ähnlich wie in der jüdischen Kabbala gibt es auch im Hinduismus einen Teil, der sich mit Zahlen beschäftigt. So kann man im Vedischen Quadrat verborgene Muster erkennen. Beim Vedischen Quadrat handelt es sich um eine Multiplikation-Tabelle von Grundziffern, die man erhält, wenn man die Quersumme einer Zahl bildet. Das Muster zeigt sich, wenn man gleiche Grundziffern miteinander verbindet. Jede Grundziffer bildet hierin ein bestimmtes Muster. Die Grundzifferpaare, deren Summe gleich 9 ist, sind Spiegelbilder voneinander. Das gilt für 1 und 8, 2 und 7, 3 und 6, 4 und 5. Die 9 steht allein.
Grundziffern im Vedischen Quadrat
Das erinnert doch stark an den kabbalistischen Baum des Lebens, der in der Mitte des Garten Edens steht. Leider wird auf ihn und seine Bedeutung in der Bibel nicht weiter eingegangen. Dennoch möchte ich ihn an dieser Stelle kurz erwähnen, da er für die Schöpfung nicht so unwichtig zu seinen scheint, er aber im Christentum keine Bedeutung hat.
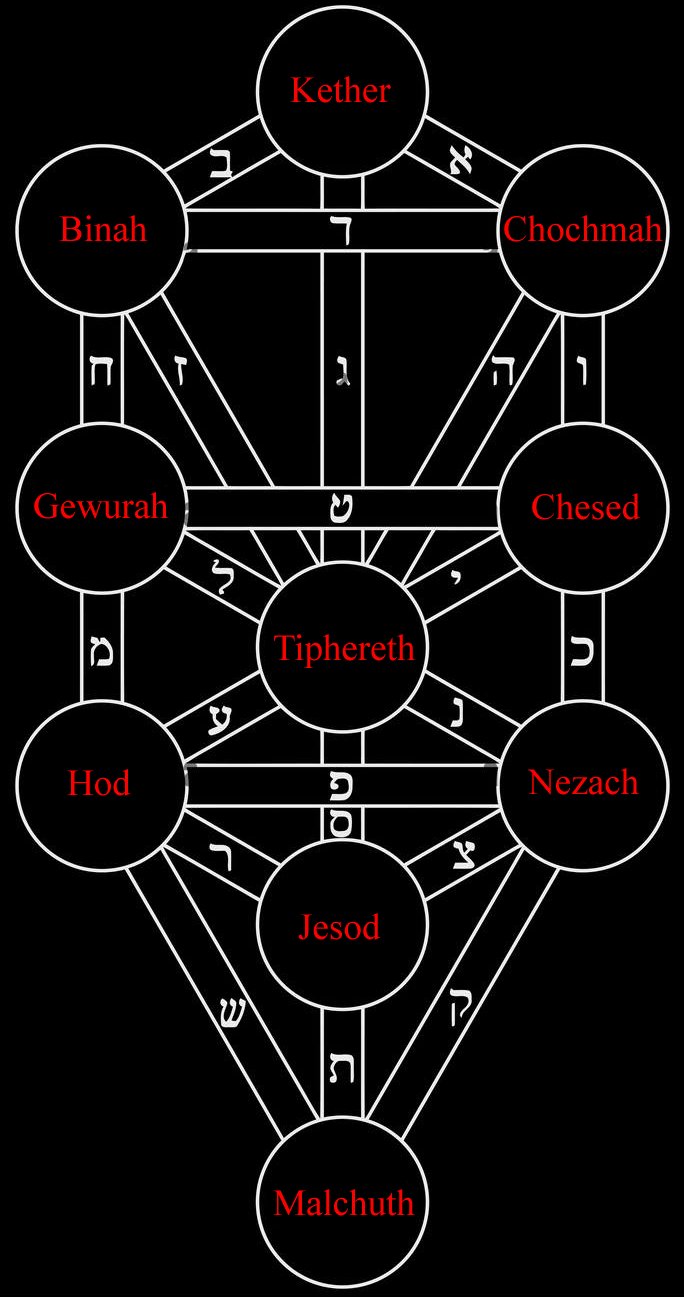
Die 22 Pfade welche, die zehn Sefiroth (Sphären) im kabbalistischen Baum des Lebens untereinander verbinden, entsprechen den Großen Arkana, den Tarot-Trümpfen. Hier entspricht der erste Pfad dem Narren, der letzte Pfad der Welt. Ausserdem findet man in der kabbalistischen Sprache auch die 72 Namen Gottes. Hier taucht wieder die 72 als heilige Zahl auf, die es auch im Islam gibt. Dort allerdings in Form von 72 Jungfrauen.
Primzahlen sind doch nicht so zufällig – die Ulam-Spirale
Im Ggensatz zu der Annahme, dass Primzahlen rein zufällig auftauchen, kann man bei genauerer Batrachtung erstaunliche Muster erkennen. Doch bevor ich diese aufdecke, möchte ich noch auf eine weitere Eigenschaft von Primzahlen hinweisen. Primzahlen enden immer auf 1, 3, 7 oder 9. Wenn Primzahlen rein zufällig auftauchen würden, sollte es egal sein, worauf die letzte Primzahl endete. Es hat sich aber gezeigt, dass zwei aufeinander folgende Primzahlen nie auf die gleiche Ziffer enden. Es hat sich vielmehr gezeigt, dass Primzahlen, die auf 3 enden häufiger nachfolgende Primzahlen besitzen, die auf 9 enden.
Der polnische Mathematiker Stanislaw Ulam machte folgende geometrische Entdeckung. Wenn man die Primzahlen spiralförmig anordnet, dann liegen diese häufig auf Diagonalen innerhalb der Spirale.
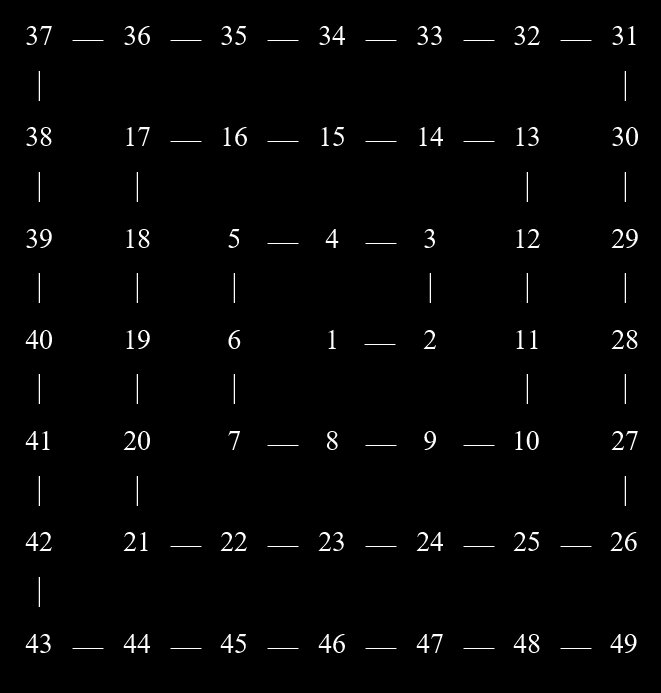
die Ulam-Spirale versteckt zwischen den natürlichen Zahlen

Die Ulam Spirale ohne die Nicht-Primzahlen
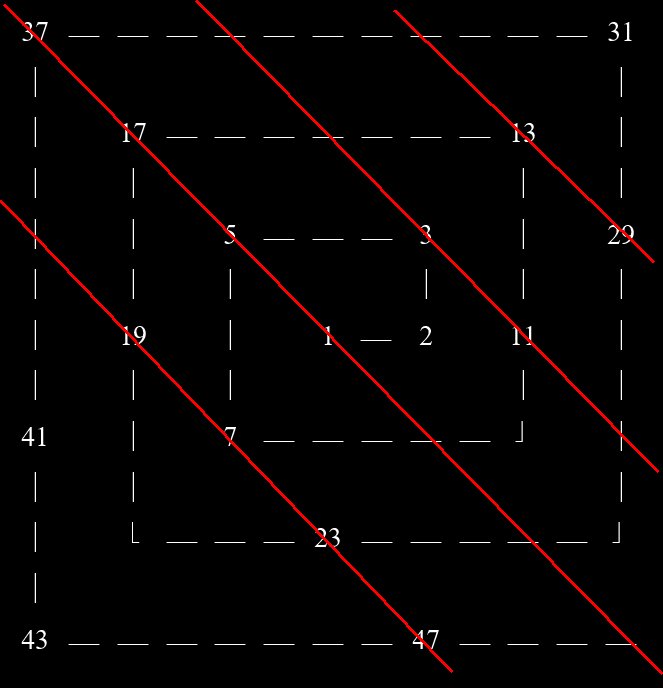
Diagonalen in der Ulam-Spirale
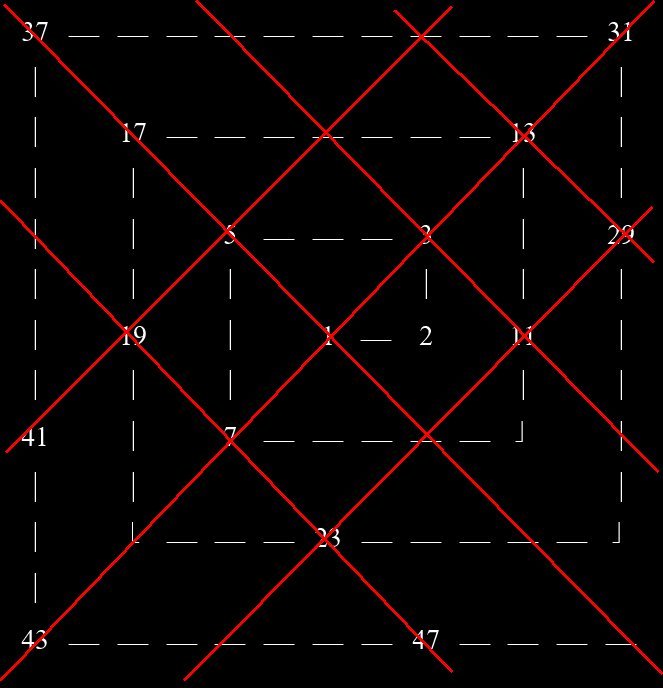
weitere Diagonalen in der Ulam-Spirale
Interessanterweise wird die 1 hierbei getroffen, obwohl sie keine Primzahl ist, die 2 hingegen nicht, obwohl sie eine Primzahl ist. Das ist auch ein Grund dafür, dass ich die 1 als Startzahl mitbetrachte. Es geht mir weniger um mathematisch einwandfreie Betrachtungen – nach Definitionen – als mehr um das Erkennen von Mustern und Strukturen.