Vater,
der Du das verborgene Licht aller Lichter,
der unwandelbare Eine hinter aller Vielfalt,
das unteilbare Substrat aller Formen, Zahlen und Klänge,
die höchste Wirklichkeit aller Namen
und das Wesen aller Geschöpfe bist –
Die sei Lob, Anbetung und Ehre.
Du, der Du das Leben alles Lebendigen,
der Quell aller Farben und Töne,
der schweigende Urgrund aller Melodien, Rhythmen und Klänge,
der Ursprung aller Sprachen und Lieder,
das eine Sein aller Namen und Formen,
der eine Schöpfer aller Geschöpfe,
die eine Wahrheit hinter allen Religionen,
das Licht unseres Leibes
und das geheime Glück unseres Herzens bist –
vor Dir verneige ich mich.
Entferne den Schleier von Unwissenheit und Verblendung,
der unsere Herzen bedeckt und
offenbare uns Dein wahres, leuchtendes Wesen,
verborgen hinter dem Glanz der Natur,
Dein erhobenes Antlitz im Wandel der Schöpfung,
Deinen weisen Plan im Gang unseres Lebens
und das Licht des Ich Bin im Brautgemach unserer Seele.

Die moderne Zahlenmystik – die geometrische Vereinigung von
Kunst und Wissenschaft
Die folgende Ausführungen basieren auf dem Buch Philomath von Robert Edward Grant.
Aus kopierschutzrechtlichen Gründen habe ich die Abbildungen, die in dem Buch zu finden sind zum Teil per Hand nachgezeichnet.
Der Schlüssel zum tieferen Verständnis der Schöpfung
– I –
Seit Anbeginn der Zeit haben die Menschen gezählt. Sie zählten ihre Finger und Dinge ihres Haushalts sowie ihr Vieh. Sie zählten die Tage, Wochen und Monate, um zu wissen, wann die Zeit der nächsten Aussaat gekommen war.
Ob bewusst oder unbewusst, die Idee von Zahlen war schon immer im menschlichen Geist verankert. Im Alten Testament findet man die Zeile: „Die Macht Israels kommt von den Zahlen, denn Gott hat alles mit Gewicht, Maß und Zahl gemacht.“ (Buch Numeri). Und Pythagoras Sagte: „Die Zahl ist der Vater der Götter und der Menschen.“ Überall in der Schöpfung lassen sich Zahlenverhältnisse erkennen, die wunderbar anmuten. Bereits in früheren Zeiten haben die Menschen den Zahlen daher magische Kräfte zugeordnet.
Ursprünglich wurden Zahlen in begrenzten Begriffen wie eins, zwei und viele ausgedrückt. Seitdem haben sie sich jedoch stark vermehrt und sich bis ins Unendliche ausgedehnt.
Die Beziehungen, welche die Menschen zwischen der Welt um sie herum und den Zahlen fanden, waren vielfältig und führten oft zu grundlegenden Erkenntnissen. Von ihren eigenen Körperteilen über Pflanzen und ihre Samen und deren Erträge bis hin zu den Zyklen des Mondes und den Perioden der Sonne und der Planeten, erweckte alles in ihnen ein Gefühl für eine Verbindung mit der Schöpfung. Darüber hinaus erkannten sie, dass Geometrie und Zahlen keine getrennten Einheiten sind, sie sind eng miteinander verbunden und verknüpft.
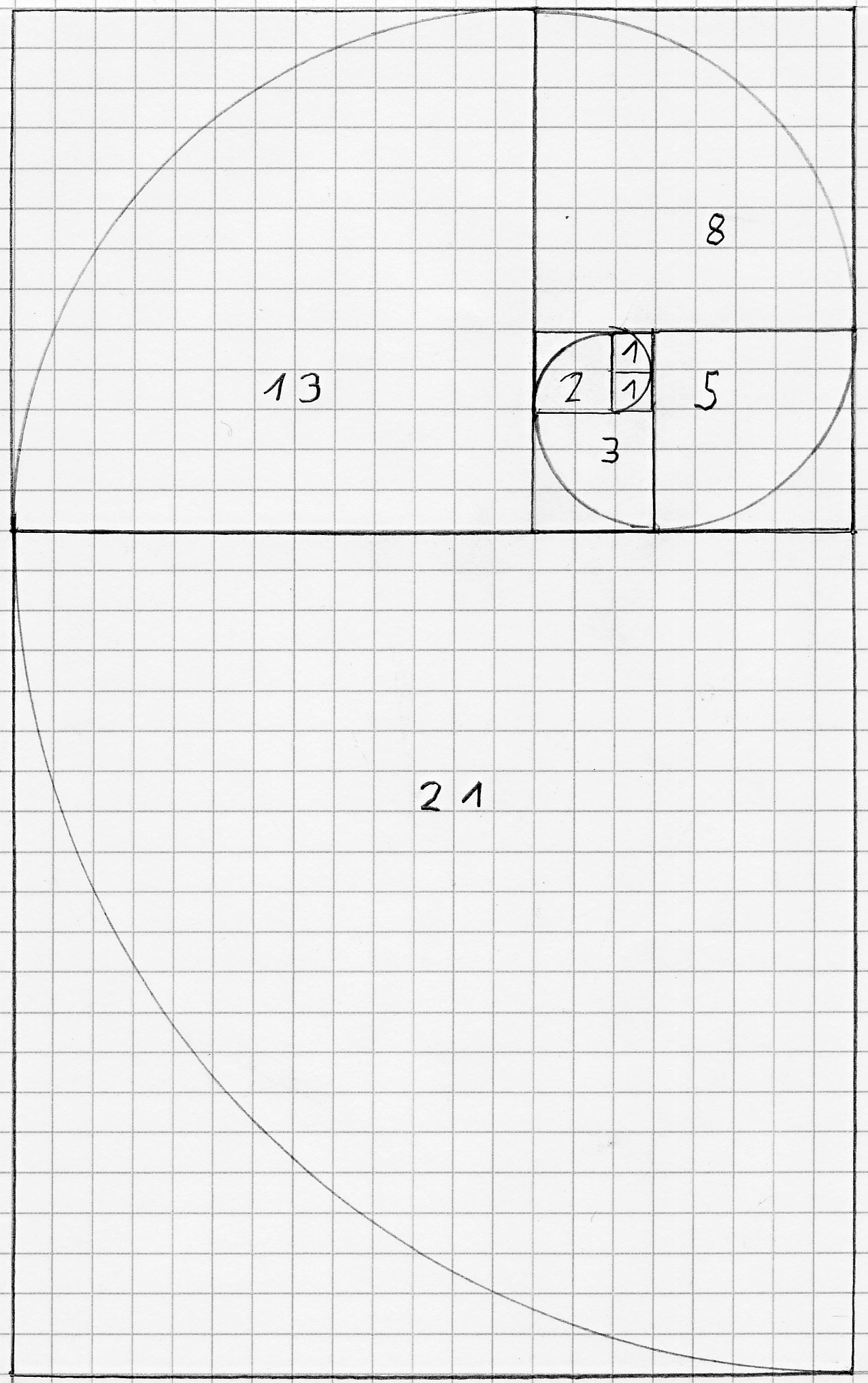
Die Fibonacci-Folge ist in ihrem Wesen nach rein numerisch, sobald ihre Zahlen jedoch in die Form von Quadraten abgebildet werden, lässt sich darin eine wunderschöne Spirale erkennen, die in der Natur in Hülle und Fülle vorkommt.
Die hier dargestellt Spirale beruht auf der Fibonacci-Folge:
1, 1 , 2, 3, 5, 8, 13, 21, …
Fundamentalkonstanten wie Pi und der Goldene Schnitt Phi sind unendliche Zahlen, die geometrische Formen und ihre Ausdehnungen bestimmen. Tatsächlich basieren die Formen und Proportionen einer Gestalt, die bei uns Menschen Anklang findet, fast immer auf „magischen Zahlen“ oder fundamentalen Konstanten, wie der Quadratwurzel aus 2 oder auch Naturkonstanten, wie der Lichtgeschwindigkeit c.
Wenn man glaubt, dass Zahlen und Geometrie aus derselben Quelle stammen, gibt es vielleicht auch einen Grund dafür, dass bestimmte Muster in der Natur immer wieder auftauchen. So sehen die Menschen in der Natur viele Rätsel oder auch eine göttliche Verschlüsselung. Doch die Schlüssel zum tieferen Verständnis der Natur findet man überall verteilt. Sie sind verborgen in den komplexen Mustern und Formen der Natur, die wir durch unsere Sinne wahrnehmen können.
So wie wir geometrische Muster durch unsere Augen wahrnehmen, werden sie in unserem Gehirn mit Zahlen verknüpft, wie die Zahl 3 für ein Dreieck oder die Zahl 4 für ein Quadrat. Die Formen, die nicht als solche beschrieben werden können, werden meist als zufällig oder ungleichmäßig angesehen.
Im Folgenden geht es um die Entschlüsselung des göttlichen Codes der Schöpfung. Es geht darum verborgene Strukturen und Muster in der Natur zu entdecken, um so ein tieferes Verständnis der Schöpfung zu erlangen.
Über die Eigenschaften von Zahlen
Wir beginnen die Suche nach den tieferen Mustern und Strukturen der Schöpfung, indem wir Zahlen größer als 0 auf eine einzige Ziffer reduzieren. Diese erhalten wir dadurch dass, wir die Quersumme der jeweiligen Zahl bilden. Dieses Verfahren wiederholen wir so oft, bis nur noch eine Ziffer übrig bleibt.
Die Quersumme einer Zahl Q(X) erhalten wir indem wir die Summe der einzelnen Ziffern der Zahl X bilden.
Beispiel: Wir bilden die Quersumme der Zahl 6821 → Q(6821) = 6 + 8 + 2 + 1 = 17
Da die Zahl 17 als erste Quersumme von 6821 aus 2 Ziffern besteht, wenden wir das Verfahren noch einmal an,
wir bilden also die Quersumme von 12 → Q(12) = 1 + 2 = 3
Die Quersumme von 6821 ist letztendlich 3.
Dieses Verfahren funktioniert auch mit endlichen Dezimalbrüchen.
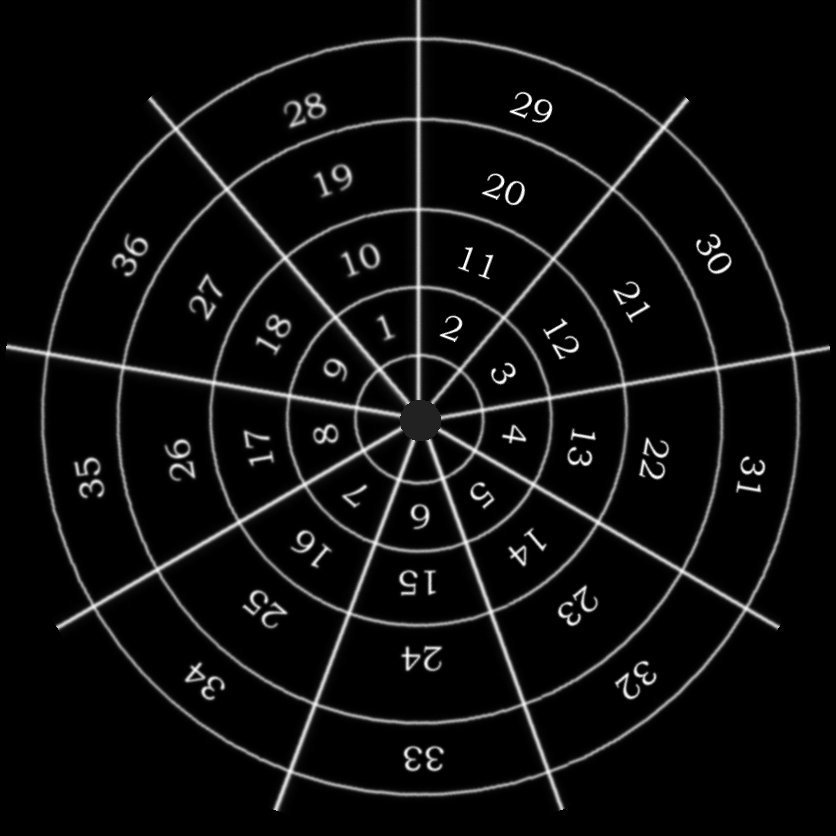
Durch das Quersummen-Verfahren erhalten wir nur Werte von 1 bis 9. Die Null kommt nicht vor, da wir nur Zahlen betrachten, die größer sind als Null. Die so entstandenen Ziffern bezeichnen wir als Grundziffern. Es entsteht folgendes Bild, bei dem Zahlen, die übereinander stehen, die gleiche Quersumme besitzen:
Das Rad der Grundziffern
Die Grundrechenarten im Rad der Grundziffern
Addition und Subtraktion:
Wenn a + b + c + … = d, dann ist Q[ Q(a) + Q(b) + Q(c) + … ] = Q(d).
Beispiel:
687 + 5210 + 847 = 6744
→ Q(687) + Q(5210) + Q(847) = 21 + 8 + 19 = 48 → Q(48) = 12 → Q(12) = 3
und Q(6744) = 21 → Q(21) = 3
Die Summe der einzelnen Quersummen ist also gleich der Quersumme der Summe der addierten Zahlen.
Analog verhält es sich bei der Subtraktion.
Multiplikation:
Wenn a x b x c = d, dann ist Q[ Q(a) x Q(b) x Q(c) x … ] = Q(d).
Beispiel: 35 x 23 x 342 = 275310
→ Q(35) = 8 und Q(23) = 5 und Q(342) = 9 → Q(8 x 5 x 9) = Q(360) = 9
und Q(275310) = 18 → Q(18) = 9
Division:
Bei der Division verhält es sich nicht ganz so einfach, weshalb ich hier nicht weiter darauf eingehe.
Die besondere Bedeutung der 9
Da die 0 unter den Grundziffern nicht vorkommt, übernimmt die 9 hier die Aufgaben der 0.
Addiert man die 9 zu einer beliebegen Zahl, verändert sich nicht ihre Grundziffer. Beispiel: Q(34) = 7, Q(34 + 9) = Q(43) → Q(43) = 7
Bei der Multiplikation einer Zahl mit 9, erhält man für die Grundziffer immer 9. Genauso wie man bei der „echten“ Multiplikation mit 0 immer 0 erhält.
Beispiel: 56 x 9 = 504 → Q(504) = 9 und 57 x 9 = 513 → Q(513) = 9
Die 9 stand symbolisch immer schon für Vollständigkeit. Sie steht für den Anfang und das Ende von Zeitaltern. So wandert der Tierkreis alle 72 Jahre um ein Grad durch den Nachthimmel. Q(72) = 9 ein voller Umlauf dauert (360 x 72) = 25920 Jahre dabei ist Q(25920) = 9
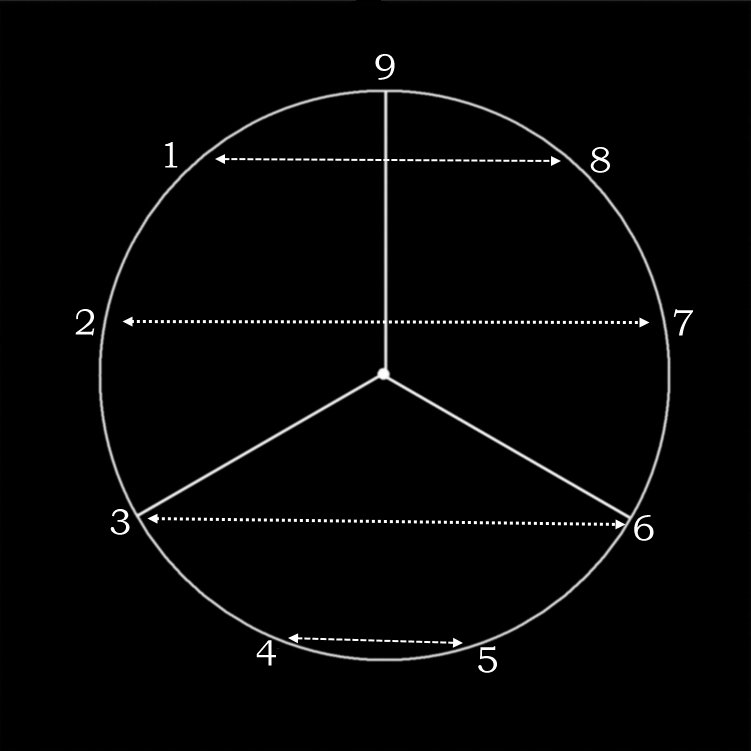
Der Kreis der Grundziffern
Wenn wir die Grundziffer wie in folgendem Kreis anordnen, können wir einige interessante Eigenschaften erkennen. So teilen die Ziffern 3, 6 und 9 den Kreis in drei Segmente, wobei die Summe der Ziffern in jedem Segment wieder gleich 3, 6 oder 9 ist.
Q(1 + 2) = 3
Q(4 + 5) = 9
Q(7 + 8) = 15 → Q(15) = 6
Der Kreis der Grundziffern
Außerdem ist die Quersumme von Ziffern, die sich gegnüber liegen wieder gleich 9.
Q(1 + 8) = 9
Q(2 + 7) = 9
Q(3 + 6) = 9
Q(4 + 5) = 9
Der unendliche Weg durch den Kreis der Grundziffern
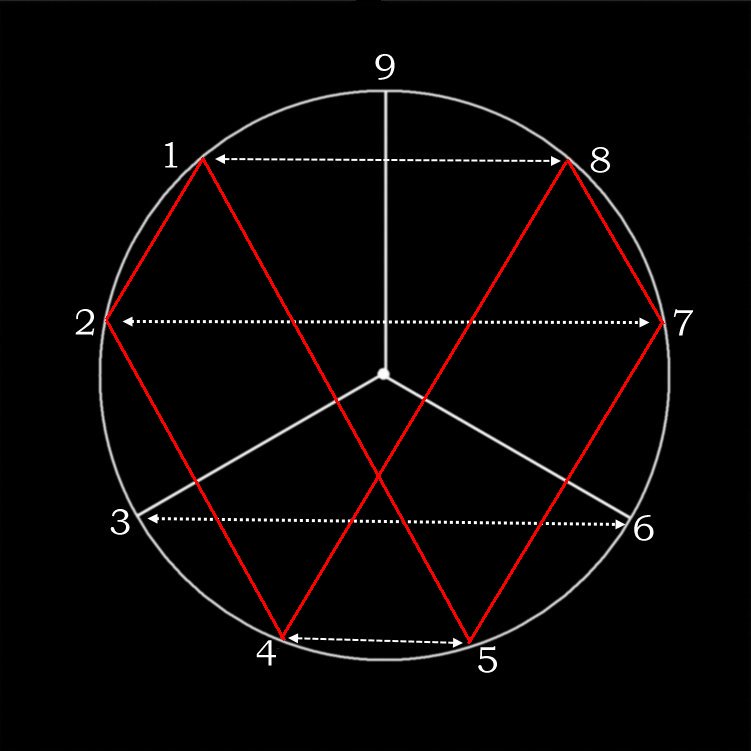
Es gibt einen unendlichen Weg durch den Kreis der Grundziffern, der sich in der Verdoppelung der Grundziffern offenbart. Wir starten bei der 1, verdoppeln diese und erhalten 2. Nun verdoppeln wir die 2 und erhalten 4. Das Verdoppeln der 4 bringt uns zur 8. Wenn wir nun 8 verdoppeln, erhalten wir 16. Die 16 kommt nicht vor, aber Q(16) ist gleich 7. Wir gehen also von der 8 zur 7. Die Verdoppelung von 7 bringt uns zur 14, die ebenfalls nicht vorkommt, aber auch hier gilt, Q(14) ist gleich 5. So kommen wir von der 7 zur 5. Das Verdopeln der 5 ergibt 10, die wieder nicht vorkommte, doch Q(10) ist gleich 1. Der Weg führt also von der 5 zurück zur 1 und der Kreis schließt sich.
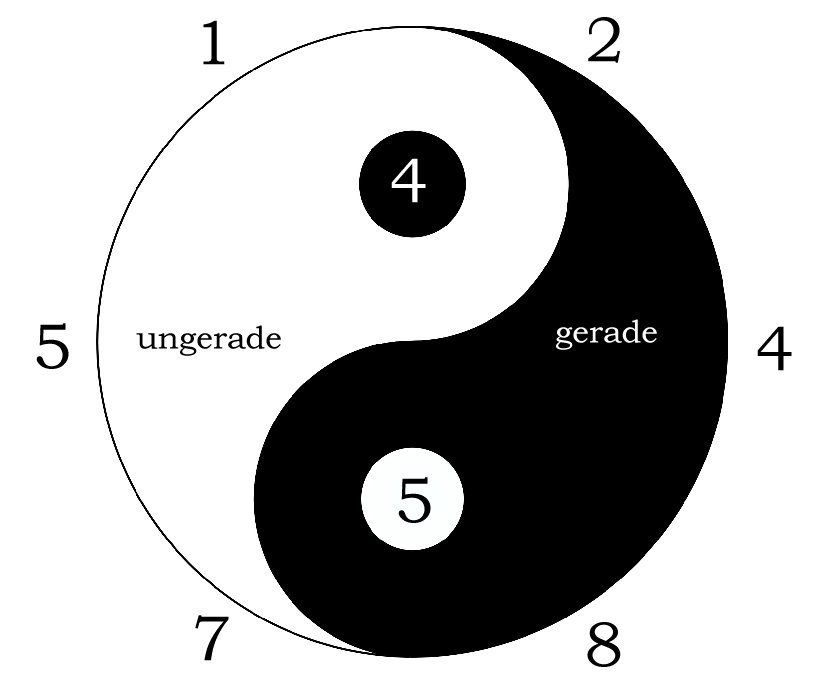
Yin und Yang
Wenn man den Kreis der verdoppelten Grundziffer in der richtigen Reihenfolge – 1, 2, 4, 8, 7, 5, 1 – anordnet, erhält man das Symbol für Yin und Yang. Auf der dunklen Seite stehen die geraden Zahlen, auf der hellen Seite die ungeraden. Wenn wir nun die Summe der geraden Zahlen bilden, erhalten wir 2 + 4 + 8 = 14 und Q(14) = 5. Aus der Summe der geraden Zahlen entsteht eine ungerade Zahl. Und wenn wir die Summe der ungeraden Zahlen bilden erhalten wir 1 + 5 + 7 = 13 und Q(13) = 4. Wir erhalten eine eine gerade Zahl. Dabei gilt: 4 + 5 = 9
Auch die Zahlen, die sich diagonal gegenüber liegen – also immer eine gerade Zahl und eine ungerade Zahl ergeben die Summe 9.
1 + 8 = 9
2 + 7 = 9
4 + 5 = 9
5 + 4 = 9
7 + 2 = 9
8 + 1 = 9
Im Diagramm von Yin und Yang werden die wirkenden Kräfte der Welt, wie weiblich und männlich, positiv und negativ, gleichwertig und ausgewogen dargestellt. Man findet diese beiden Prinzipien in allem, was existiert. Weil Yin und Yang nicht statisch sind, sondern sich ständig gegenseitig beeinflussen, sieht man in dem Diagramm den Keim des einen in seinem Gegenpol enthalten. In dem Diagramm erkennt man dies an dem schwarzen Punkt im weißen Feld und dem weißen Punkt im schwarzen Feld. Das Symbol von Yin und Yang steht für Vollständigkeit. Wobei in den Gegensätzen der Kern des Anderen steckt, was zusammen die Einheit zeigt. Die Zahlen offenbaren uns hier eine alte Weisheit.
Die Magie der Primzahlen
Wir können die Zahlen nicht nur in gerade und ungerade unterteilen, sondern wir können sie in Primzahlen und zusammengesetzte Zahlen unterteilen. Primzahlen sind natürliche Zahlen, die genau 2 Teiler haben. Sie sind durch 1 und sich selbst teilbar. Die 1 ist keine Primzahl, da sie nur einen Teiler hat. Somit ist die 2 die kleinste Primzahl und sie ist die einzig gerade Primzahl. Alle geraden Zahlen mit Ausnahme der 2 sind keine Primzahlen, sondern Vielfache von 2. Um aber die Muster und Strukturen innerhalb der natürlichen Zahlen zu verdeutlichen, soll die 1 als „Startzahl“ mit betrachtet werden. Wenn ich also im folgenden von Primzahlen spreche, mag es vorkommen, dass auch die 1 mit aufgeführt wird. Das ist mathematisch nicht einwandfrei, aber für die Mustererkennung aussagestärker. Es geht hier auch nicht um klare mathematische Beweise, sondern um das Aufzeigen von verborgenen Mustern.
Zusammengesetzte Zahler, sind Zahlen die keine Primzahlen sind. Sie haben also mindestens 3 Teiler. Die 1 als kleinsten Teiler einer Zahl und die Zahl selbst als größten Teiler der Zahl nennen wir triviale Teiler. Hat eine Zahl neben den trivialen Teilern noch mindestens einen weiteren Teiler, sprechen wir bei der Zahl von einer zusammengesetzten Zahl.
Schauen wir uns zunächst einige Teilermengen von Zahlen an. Dabei ist Tx die Teilermenge der Zahl x.
T1 = {1}
T2 = {1, 2} – Primzahl
T3 = {1, 3} – Primzahl
T4 = {1, 2, 4} – zusammengesetzte Zahl
T5 = {1, 5} – Primzahl
T6 = {1, 2, 3, 6} – zusammengesetzte Zahl
T7 = {1, 7} – Primzahl
T8 = {1, 2, 4, 8} – zusammengesetzte Zahl
T9 = {1, 3, 9} – zusammengesetzte Zahl
T10 = {1, 2, 5, 10} – zusammengesetzte Zahl
T11 = {1, 11} – Primzahl
T12 = {1, 2, 3, 4, 5, 6, 12} – zusammengesetzte Zahl
Was wir über Primzahlen wissen
- Es gibt unendlich viele Primzahlen.
- Und es gibt keinen Algorithmus, mit dem man Primzahlen herstellen kann.
- Es ist uns auch nicht möglich, zu sagen wann die nächste Primzahl auftauchen wird.
- Aufgrund der Nicht-Vorhersagbarkeit des Auftauchens von Primzahlen, werden Primzahlen häufig zum Schutz im IT-Bereich genutzt oder beim Verschlüsseln von Nachrichten.
Semiprimzahlen
Zahlen, die aus dem Produkte zweier Primzahlen entstanden sind, heißen Semiprimzahlen. Sie haben mindestens 3 und höchstens 4 Teiler.
Beispiele:
2 x 2 = 4 → T4= {1, 2, 4}
2 x 3 = 6 → T6 = {1, 2, 3, 6}
3 x 3 = 9 → T9 = {1, 3, 9}
3 x 5 = 15 → T15 = {1, 3, 5, 15}
173 x 179 = 30967 → T30967 = {1, 173, 179, 30967}
997 x 997 = 994009 → T997 = {1, 997, 994009}
30967 und 994009 sind Semiprimzahlen, die wir ganz einfach hergestellt haben. Die Teiler der Zahlen über die Primfaktorzerlegung zu ermitteln ist dann aber nicht so einfach. ChatGPT hat 30967 als Primzahl identifiziert, was falsch ist. DeepSeek hat 30967 als Semiprimzahl identifiziert und gezeigt, dass 30967 = 173 x 179. Hier kommt die KI also z.T. an ihre Grenzen.
Muster oder Zufall?
Nun stellen wir uns die Frage, ob die Verteilung der Primzahlen einem Muster folgt oder ob sie rein zufällig auftrtreten.
Jede Primzahl > 5 endet auf 1, 3, 7, 9.
Jede Primzahl > 5 kann in der Form 6k + 1 oder 6k – 1 dargestellt werden, wobei k eine natürliche Zahl ist. Das bedeutet nicht, dass ich über diese beiden Formeln beliebige Primzahlen herstellen kann. Es gilt nur anders herum. Wenn ich eine Primzahl habe, dann kann ich sie über eine der beiden Formeln darstellen.
Beispiele:
7 = 6 x 1 + 1
11 = 6 x 2 – 1
13 = 6 x 2 + 1
17 = 6 x 3 – 1
19 = 6 x 3 + 1
23 = 6 x 4 – 1
29 = 6 x 5 – 1
Abgesehen davon, dass die 6 eine entscheidende Bedeutung für Primzahlen zu haben scheint, gilt auch: p2 = f x 24 + 1 für alle Primzahlen p ≥ 5 wobei f eine natürliche Zahl ist.
Erklärung:
Der Faktor k in p = 6k ± 1 kann gerade oder ungerade sein. Wenn wir nun k durch 2m für gerade Zahlen ersetzen und durch 2m + 1 für ungerade Zahlen ersetzen, und dann die Gleichung quadrieren, erhalten wir folgende 4 Fälle:
p2 = ((6 x 2m) + 1)2 = (12m + 1)2 = 144m2 + 24m + 1
p2 = ((6 x 2m) – 1)2 = (12m – 1)2 = 144m2 – 24m + 1
p2 = (6 x (2m + 1) +1)2 = (12m + 7)2 = 144m2 + 168m + 49
p2 = (6 x (2m + 1) -1)2 = (12m + 5)2 = 144m2 + 120m + 25
Alle ausmultiplizierten Gleichungen erhalten den Faktor 24 x am + 1, wobei a eine natürliche Zahl ist, wie z.B. in (6m2 + m) x 24 +1.
Setzen wir jetzt (6m2 + m) = f, erhalten wir wieder p2 = f x 24 + 1.
Eine weitere Eigenschaft von Primzahlen ist die, dass ale Primzahlen, die größer als 3 sind, Quersummen besitzen, die nur die Werte 3, 6 oder 9 haben. Aus der Gleichung p2 = f x 24 + 1 geht folgendes hervor:
Wenn p die Quersumme 3, 6 oder 9 hat, ist Q(p2) immer gleich 9, denn:
Q(32) = 9
Q(62) = Q(36) = 9
Q(92) = Q(81) = 9
Auf der rechten Seite der Gleichung haben wir f x 24 + 1, wenn wir uns nur den Teil f x 24 ansehen, so haben wir hier immer die Quersumme 3, 6 oder 9:
Q(1 x 24) = Q(24) = 6
Q(2 x 24) = Q(48) = Q(12) = 3
Q(3 x 24) = Q(72) = 9
Q(4 x 24) = Q(96) = Q(15) = 6
Q(5 x 24) = Q(120) = 3
Q(6 x 24) = Q(144) = 9
Q(7 x 24) = Q(168) = Q(15) =6
Q(8 x 24) = Q(192) = Q(12) = 3
Q(9 x 24) = Q(216) = 9
Addieren wir nun jeweils 1 hinzu, erhalten wir immer 7, 4 oder 1 als Quersumme. Wir erhalten also nie eine 9 auf beiden Seiten der Gleichung. Eine Primzahl hat also nie eine Quersumme von 3, 6 oder 9.
Um bei einer beliebigen Zahl festzstellen, ob sie eine Primzahl ist, prüfen wir erst ob es ich um eine ungerade Zahl handelt. Wenn ihre Quersumme dann weder 3 oder 6 oder 9 ist, ist die Zahl keine Primzahl. Bei allen anderen Quersummen besteht die Möglichkeit, eine Primzahl zu sein.
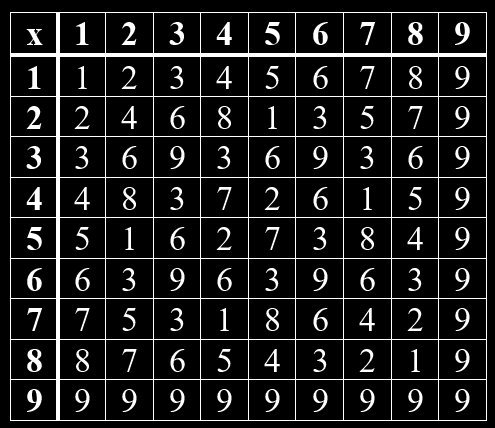
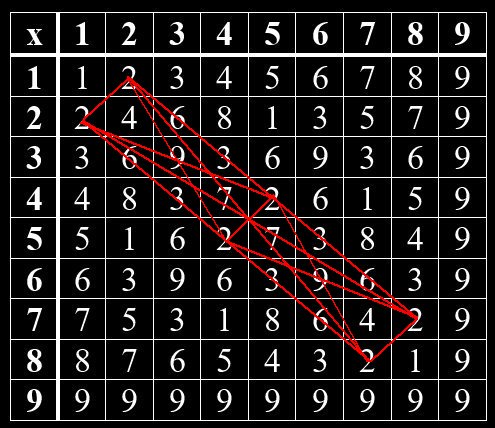
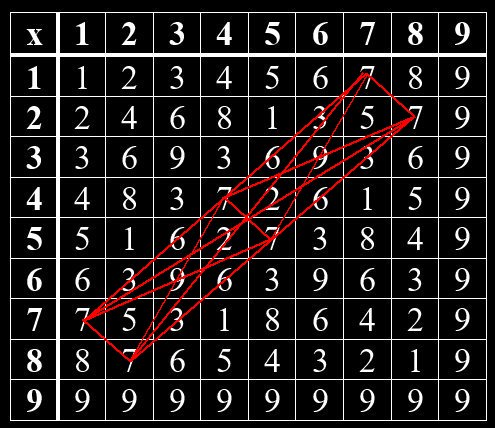
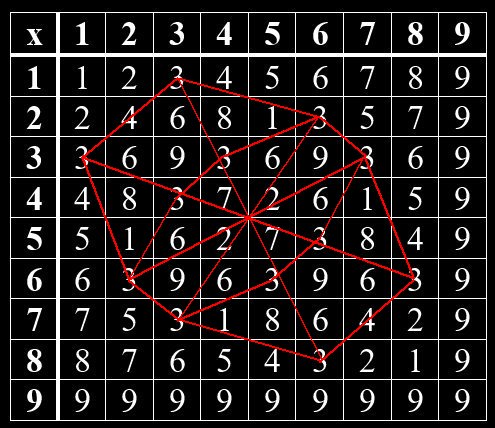
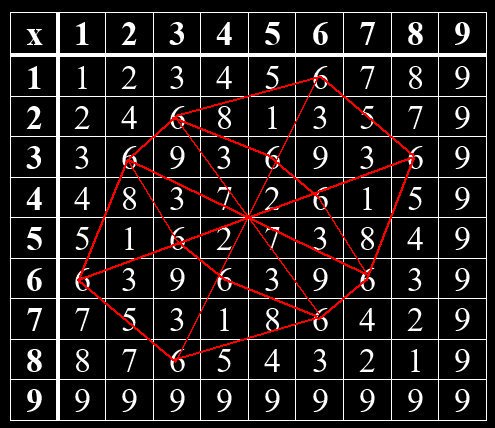
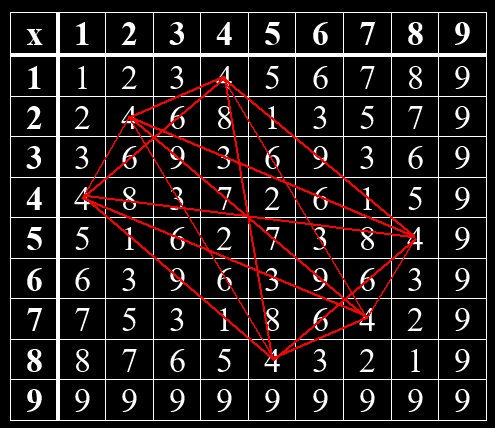
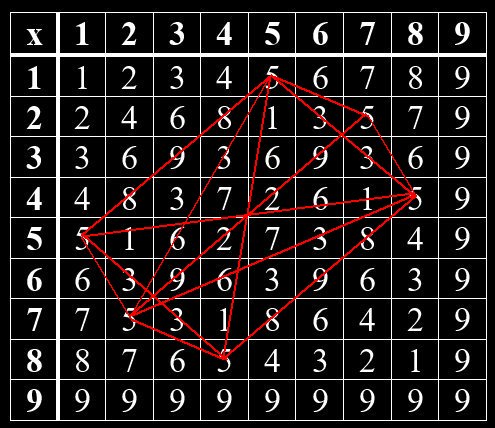
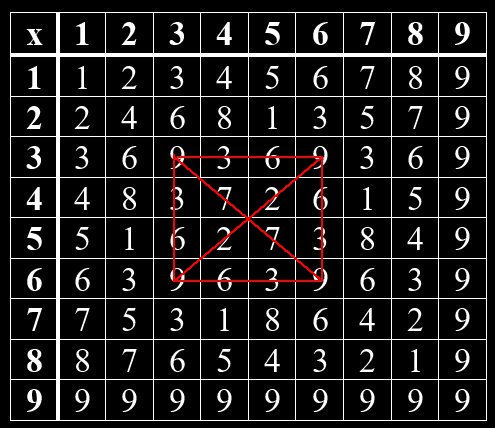
Geheime Strukturen im Vedischen Quadrat
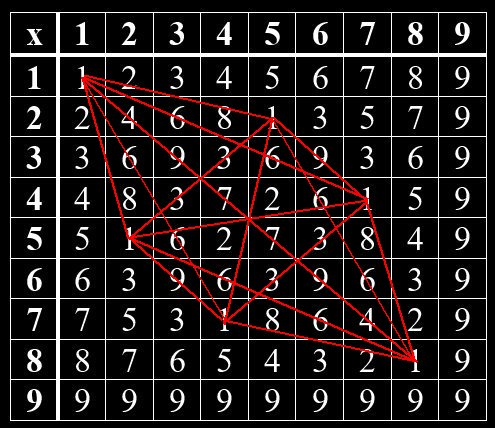
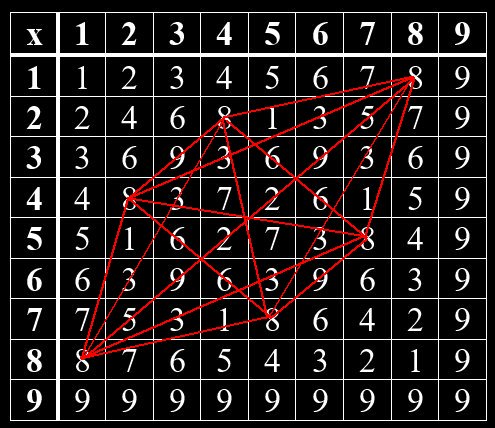
Im Hinduismus wurden mündliche Überlieferungen um 1500 -2000 v Chr. in den heiliegen Schriften – den Veden – niedergeschrieben. Ähnlich wie in der jüdischen Kabbala gibt es auch im Hinduismus einen Teil, der sich mit Zahlen beschäftigt. So kann man im Vedischen Quadrat verborgene Muster erkennen. Beim Vedischen Quadrat handelt es sich um eine Multiplikation-Tabelle von Grundziffern, die man erhält, wenn man die Quersumme einer Zahl bildet. Das Muster zeigt sich, wenn man gleiche Grundziffern miteinander verbindet. Jede Grundziffer bildet hierin ein bestimmtes Muster. Die Grundzifferpaare, deren Summe gleich 9 ist, sind Spiegelbilder voneinander. Das gilt für 1 und 8, 2 und 7, 3 und 6, 4 und 5. Die 9 steht allein.
Grundziffern im Vedischen Quadrat
Das erinnert doch stark an den kabbalistischen Baum des Lebens, der in der Mitte des Garten Edens steht. Leider wird auf ihn und seine Bedeutung in der Bibel nicht weiter eingegangen. Dennoch möchte ich ihn an dieser Stelle kurz erwähnen, da er für die Schöpfung nicht so unwichtig zu seinen scheint, er aber im Christentum keine Bedeutung hat.
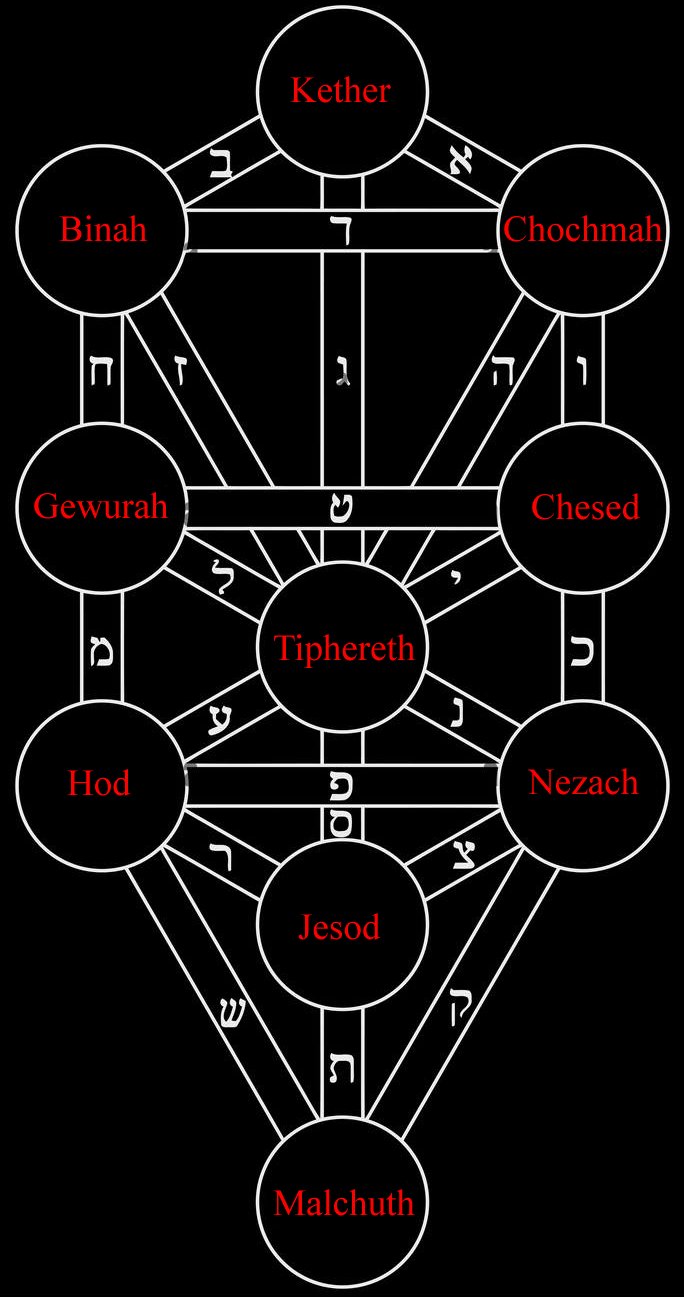
Die 22 Pfade welche, die zehn Sefiroth (Sphären) im kabbalistischen Baum des Lebens untereinander verbinden, entsprechen den Großen Arkana, den Tarot-Trümpfen. Hier entspricht der erste Pfad dem Narren, der letzte Pfad der Welt. Ausserdem findet man in der kabbalistischen Sprache auch die 72 Namen Gottes. Hier taucht wieder die 72 als heilige Zahl auf, die es auch im Islam gibt. Dort allerdings in Form von 72 Jungfrauen.